A new artificial intelligence framework developed by researchers can automatically derive fundamental physics equations directly from observational data. The model, named PhyE2E, has successfully replicated and even improved upon formulas describing complex space physics phenomena, signaling a potential new era of automated scientific discovery.
In tests using real-world astrophysical data, the system analyzed information related to solar cycles and the interplay between solar radiation, temperature, and magnetic fields. The resulting equations either matched those established by human scientists or provided a more accurate representation of the observed data, demonstrating its capacity to uncover the mathematical laws governing the universe.
Key Takeaways
- Researchers have developed an AI model called PhyE2E that can discover physics formulas from raw data.
- The system was tested on both synthetic and real astrophysical data from NASA.
- PhyE2E successfully derived an improved formula for solar cycles from data published in 1993.
- The model uses a "divide-and-conquer" method to break down complex problems into simpler, manageable parts.
- This technology could accelerate scientific discovery across various fields by automating the process of finding underlying physical laws.
Automating Scientific Discovery
The process of scientific discovery has traditionally relied on human intuition, hypothesis testing, and rigorous mathematical analysis. Scientists spend years, sometimes decades, poring over data to find patterns and formulate equations that describe physical reality. A new AI framework aims to dramatically accelerate this process.
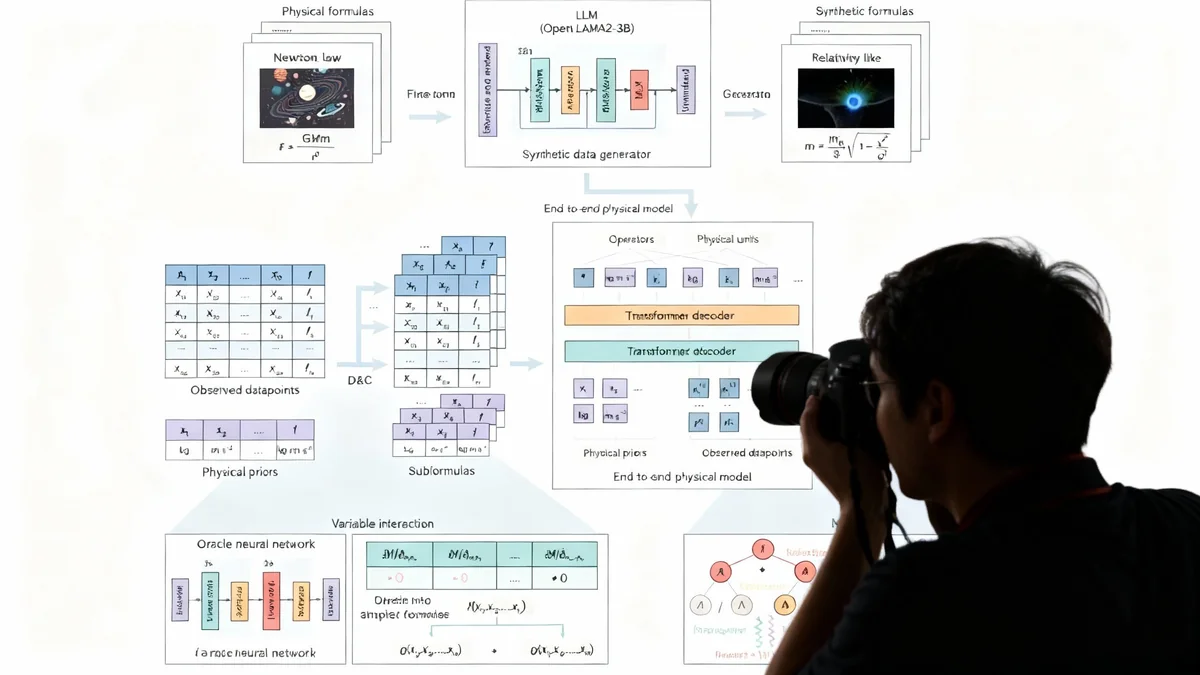
Developed by a team from Tsinghua University, Peking University, and other institutions, PhyE2E is designed to function as an automated scientist. It translates raw data points directly into compact, understandable mathematical formulas. This moves beyond simple curve-fitting, where an AI might find a line that matches data, and into the realm of genuine symbolic representation—creating equations that have physical meaning.
According to Yuan Zhou, co-senior author of the paper published in Nature Machine Intelligence, the objective was clear. "Our goal was to push AI beyond curve-fitting and toward human-understandable discovery: returning compact, unit-consistent equations that scientists can read, test, and build on," he stated.
How PhyE2E Works
The PhyE2E system employs a sophisticated, multi-stage process to transform data into knowledge. At its core is a transformer, a type of neural network architecture that excels at understanding sequences and relationships, similar to the technology behind advanced language models.
The process begins with training the model on a vast library of established physics equations. This teaches the AI what a plausible, physically consistent formula looks like. The system learns the fundamental grammar of physics, including the importance of dimensional consistency—ensuring that units like meters, seconds, and kilograms are used correctly.
A Divide-and-Conquer Strategy
One of the key innovations in PhyE2E is its 'divide-and-conquer' technique. Instead of trying to solve a complex problem in one step, the AI first analyzes the data to identify simpler, underlying relationships. It breaks the main problem into smaller sub-formulas, solves each one, and then pieces them together to form the complete equation. This methodical approach mirrors how human scientists often tackle multifaceted challenges.
Once an initial formula is generated, a refinement module using a technique called Monte Carlo Tree Search (MCTS) tidies up the expression. It adjusts constants and simplifies the structure to produce the most elegant and accurate equation possible.
"PhyE2E uses a transformer to translate data directly into a symbolic expression and its units. The result is an equation that is compact, interpretable, and dimensionally consistent."
Putting the AI to the Test
To validate its capabilities, the research team tested PhyE2E on five real-world space physics scenarios using data collected by NASA. The results were compelling. The AI was not only able to rediscover known physical laws but, in some cases, it found better ones.
One notable success involved analyzing solar cycle data originally published by NASA in 1993. When tasked with explaining the data mathematically, PhyE2E derived a new formula that provided a more accurate fit than the one previously established by physicists. It also effectively modeled the complex relationships between solar radiation, temperature, and magnetic fields—a cornerstone of space weather prediction.
Beyond Human Capability?
The ability of PhyE2E to improve upon a human-derived formula highlights a key advantage of AI in science. While human scientists are bound by existing theories and cognitive biases, an AI can explore a vast space of mathematical possibilities without preconceived notions, potentially uncovering novel relationships that were previously overlooked.
The challenge in this field is avoiding meaningless complexity. "While it's trivial to write a long expression that interpolates the data, and tempting to favor very short ones, neither guarantees physical meaning," Zhou explained. The strength of PhyE2E is its ability to learn from known physics to propose formulas that are both compact and physically plausible.
The Future of AI-Driven Science
The development of PhyE2E represents a significant step toward integrating AI as a collaborative partner in scientific research. By automating the laborious process of deriving equations from data, such tools could free up scientists to focus on higher-level conceptual work, experimental design, and interpreting the implications of new discoveries.
The framework itself is designed to be general. While its initial success was in space physics—a field with abundant, high-quality data—the researchers expect it can be adapted for other scientific disciplines, from materials science to biology.
Next Steps and Broader Goals
The team is already working on expanding the system's capabilities. Future versions will incorporate calculus-aware operators, allowing the AI to discover laws expressed as differential equations, which are common throughout physics. They also plan to improve its robustness for handling the noisier data often found in laboratory experiments.
- Calculus Integration: Enabling the discovery of laws involving derivatives and integrals.
- Noise Robustness: Improving performance with less-than-perfect experimental data.
- Cross-Disciplinary Application: Adapting the model for use in chemistry, biology, and other sciences.
Ultimately, the project is part of a broader effort to create more interpretable and reliable AI systems. By designing AI with explainability as a core principle, the researchers hope to build tools that not only make accurate predictions but also uncover the fundamental laws that make those predictions possible, deepening our understanding of the world around us.